Implicit Steerable Kernels

Abstract

Steerable convolutional neural networks (CNNs) provide a general framework for building neural networks equivariant to translations and other transformations belonging to an origin-preserving group \(G\), such as reflections and rotations. They rely on standard convolutions with \(G\)-steerable kernels obtained by analytically solving the group-specific equivariance constraint imposed onto the kernel space. As the solution is tailored to a particular group \(G\), the implementation of a kernel basis does not generalize to other symmetry transformations, which complicates the development of general group equivariant models. We propose using implicit neural representation via multi-layer perceptrons (MLPs) to parameterize \(G\)-steerable kernels. The resulting framework offers a simple and flexible way to implement Steerable CNNs and generalizes to any group \(G\) for which a \(G\)-equivariant MLP can be built. We prove the effectiveness of our method on multiple tasks, including N-body simulations, point cloud classification and molecular property prediction.

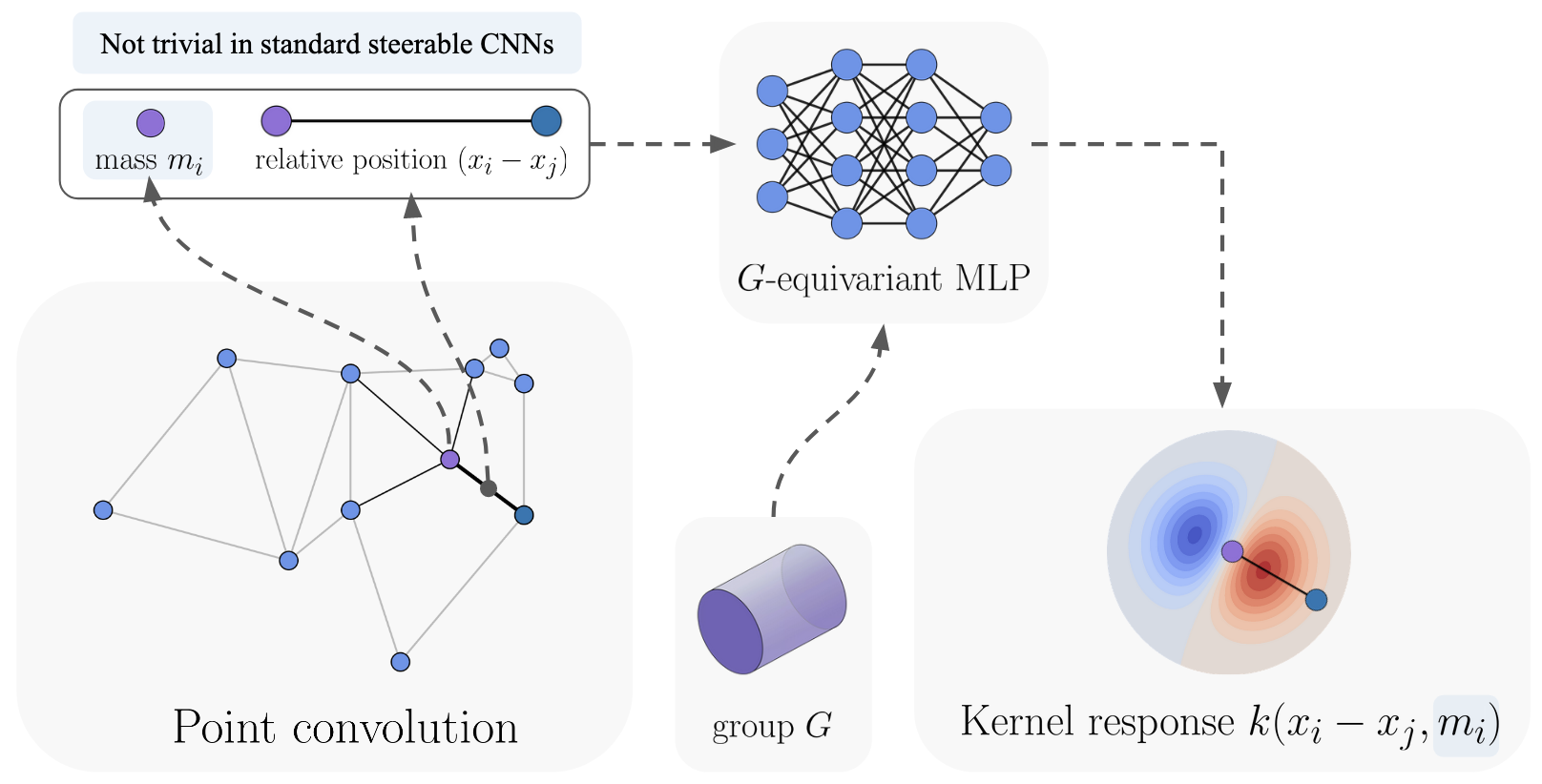
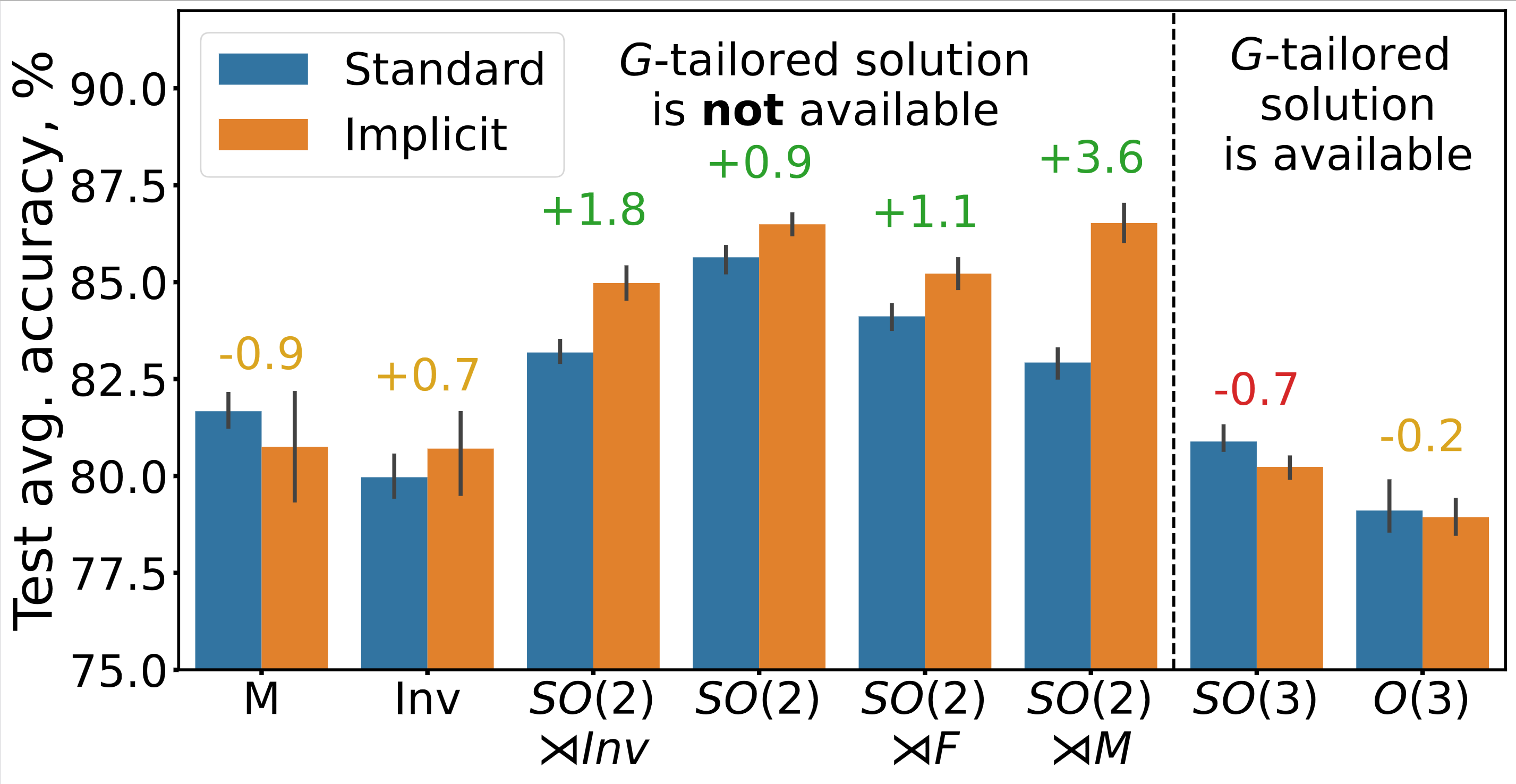
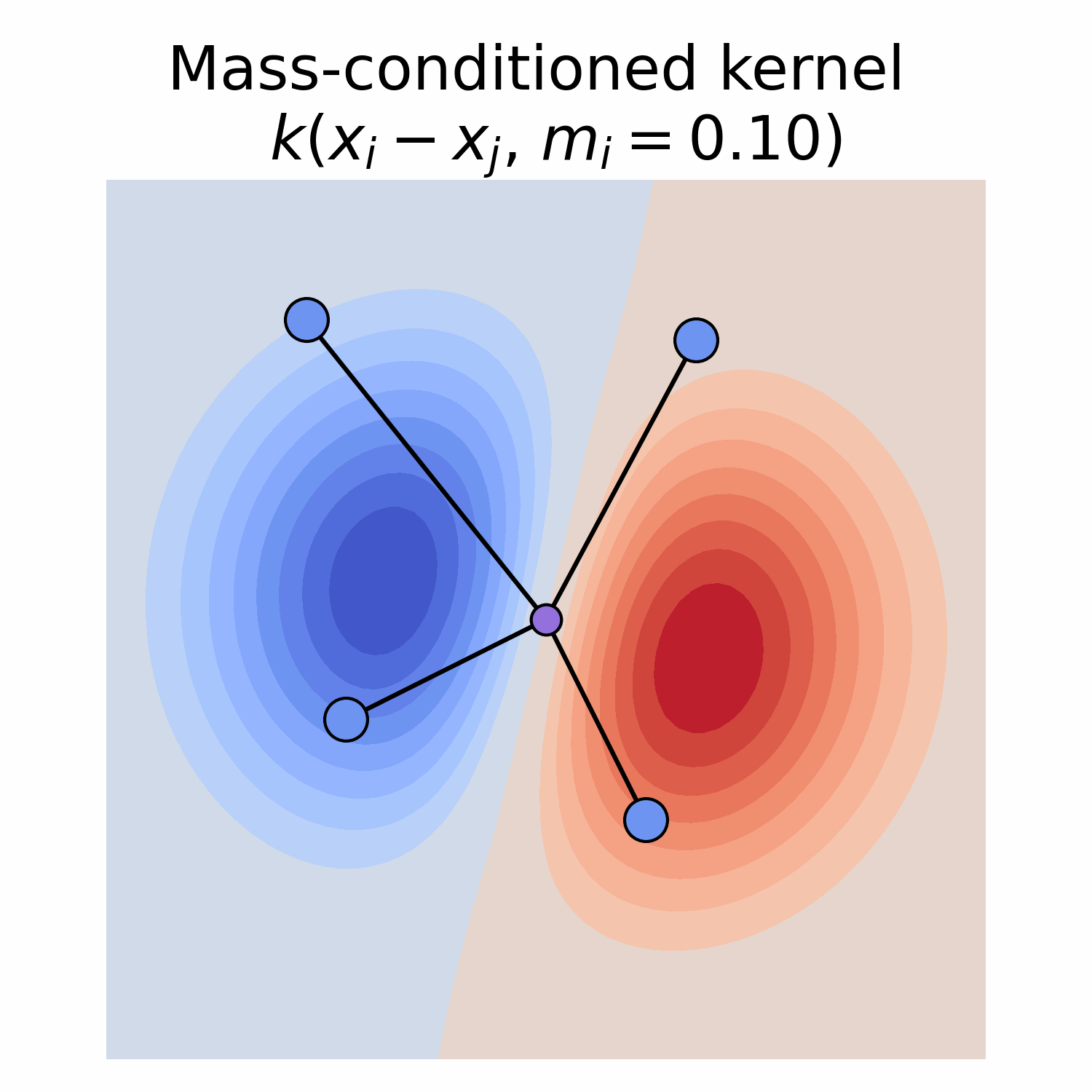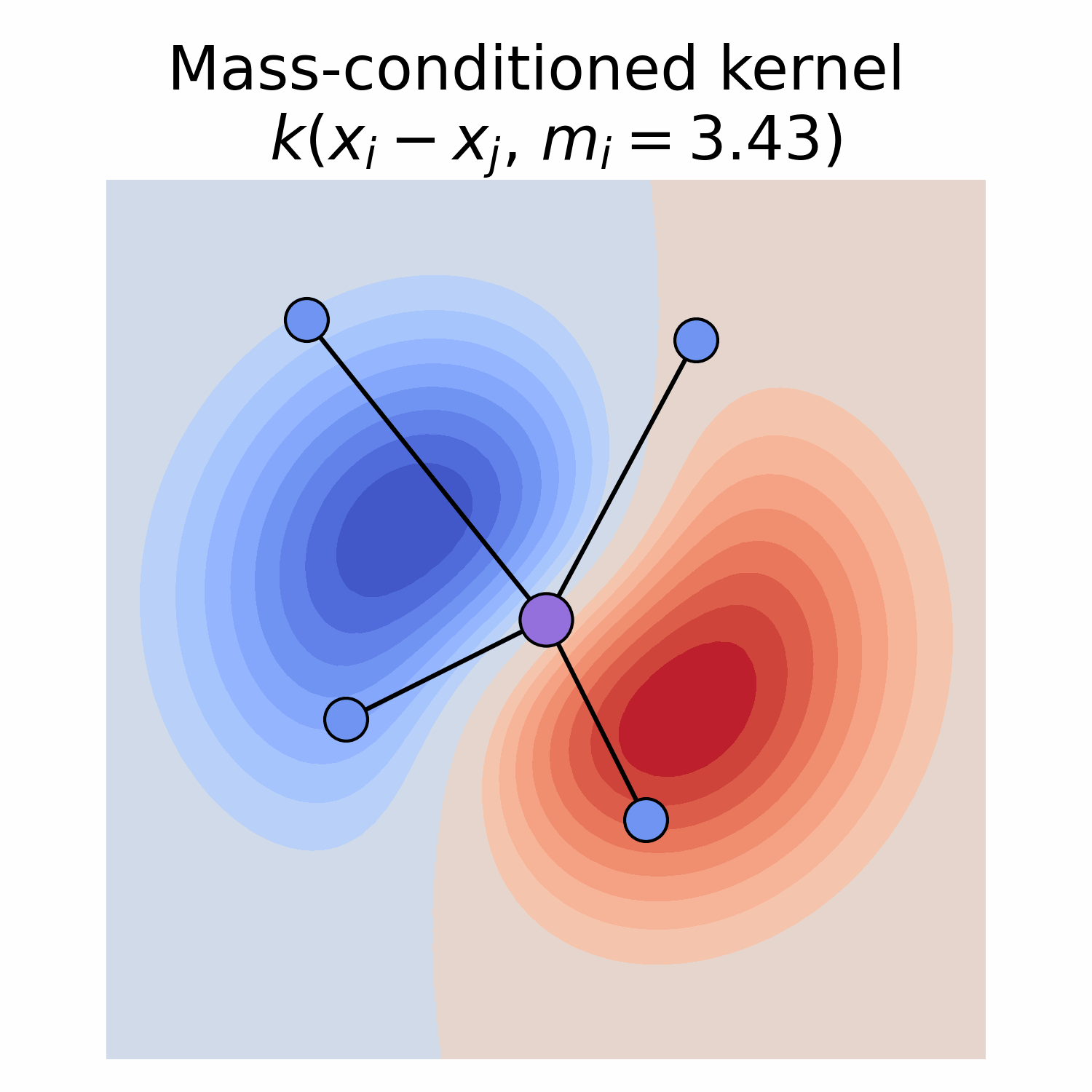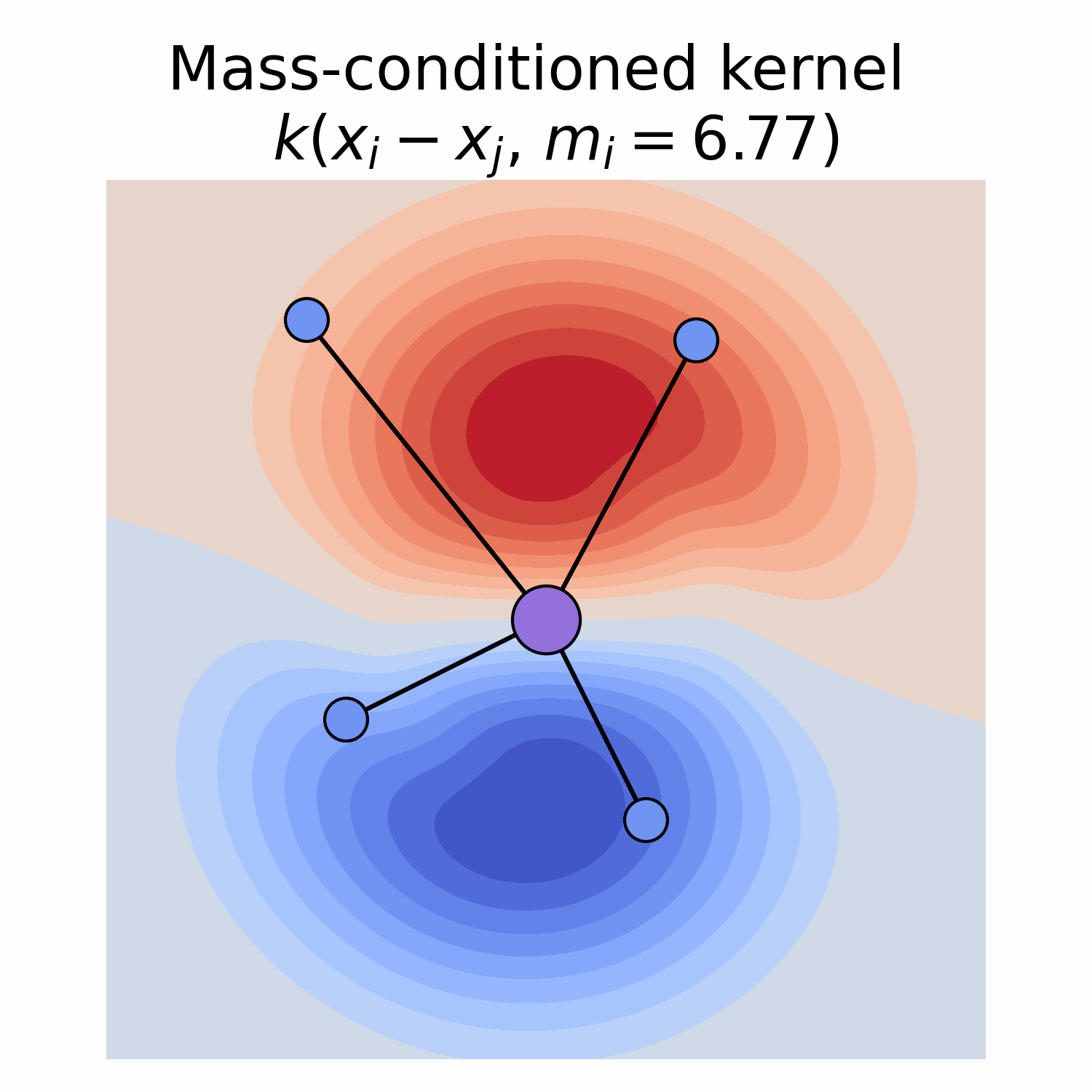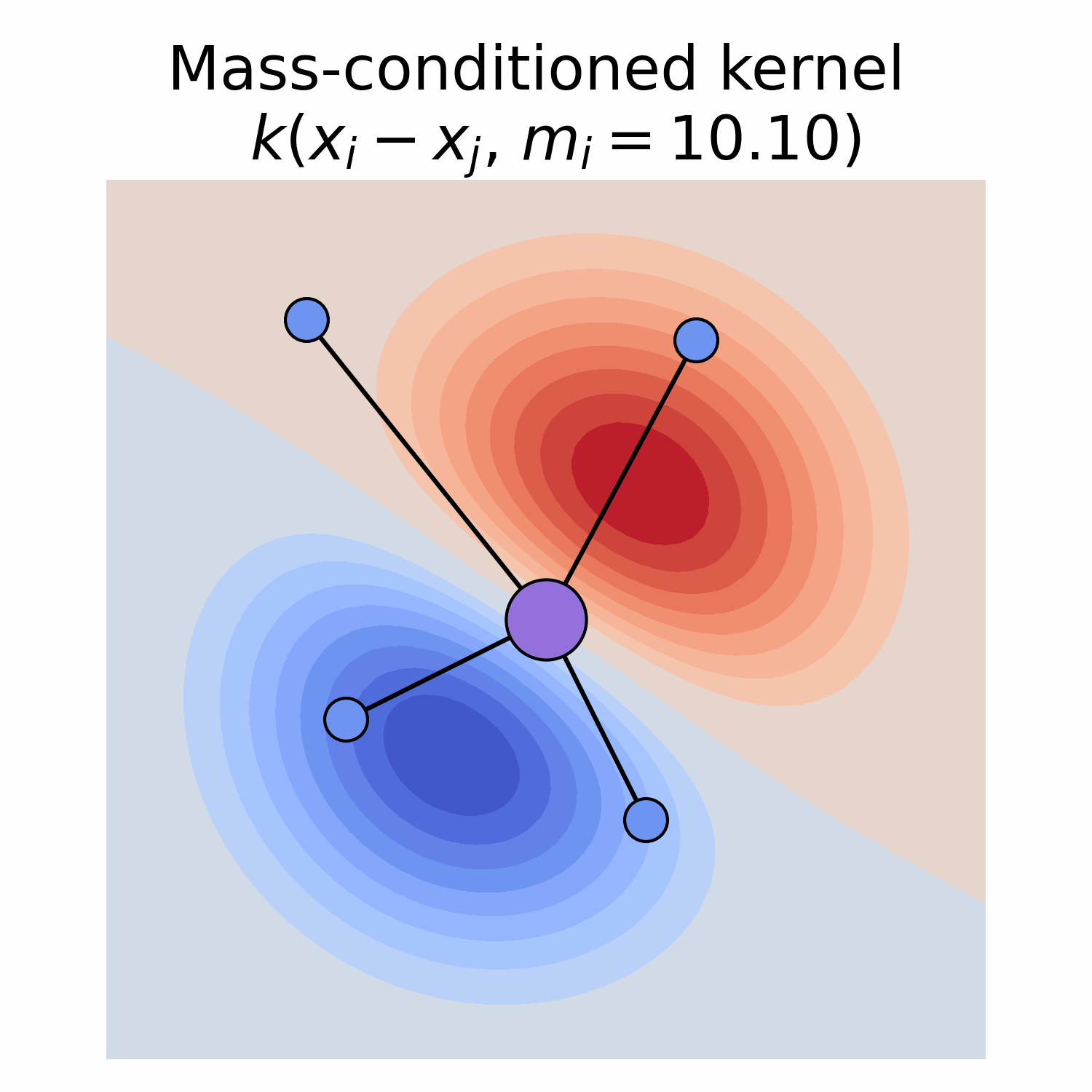
Equivariance and feature fields

From the atomic level to the vast expanse of the universe, symmetry and equivariance are consistently observed. Whether it is the behaviour of molecules or patterns in point clouds, there are often properties of the system that are preserved under certain transformations. Equivariant deep learning aims to encode these symmetries directly into the learning process, yielding more efficient and generalizable models. Such models are able to preserve certain transformations in the input data through to the model's output. 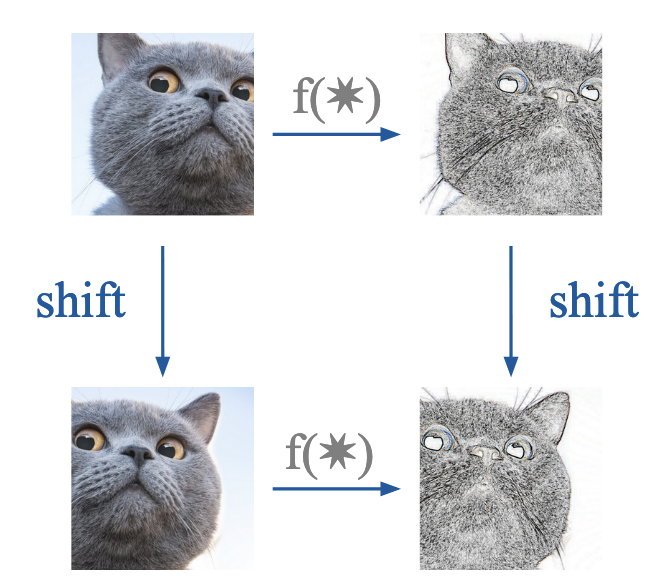Convolutional Neural Networks (CNNs) serve as a classic example, being equivariant with respect to translations in the input space (try shifting the image before and after a convolutional layer). However, to capture a broader range of symmetries found in complex systems, especially in physics and chemistry, group equivariant CNNs (G-CNNs) have been developed.

Equivariance (translation) — Equivariance of a CNN w.r.t translation (left) and rotation (right). Transforming the image before and after a convolutional layer yields the same result.

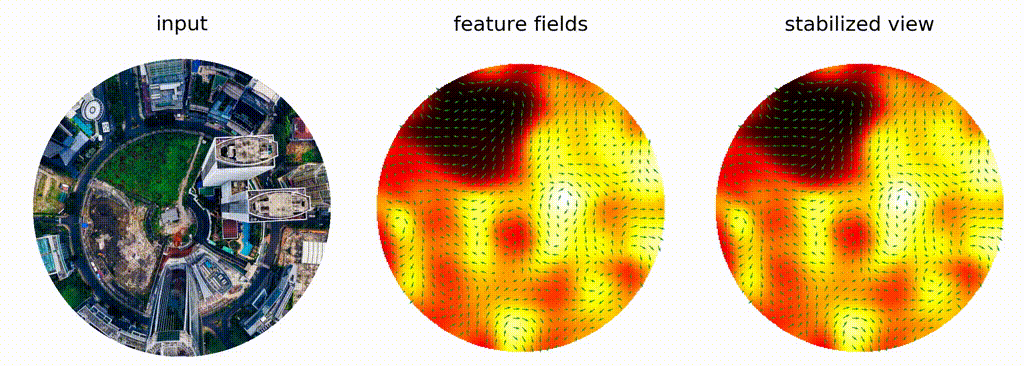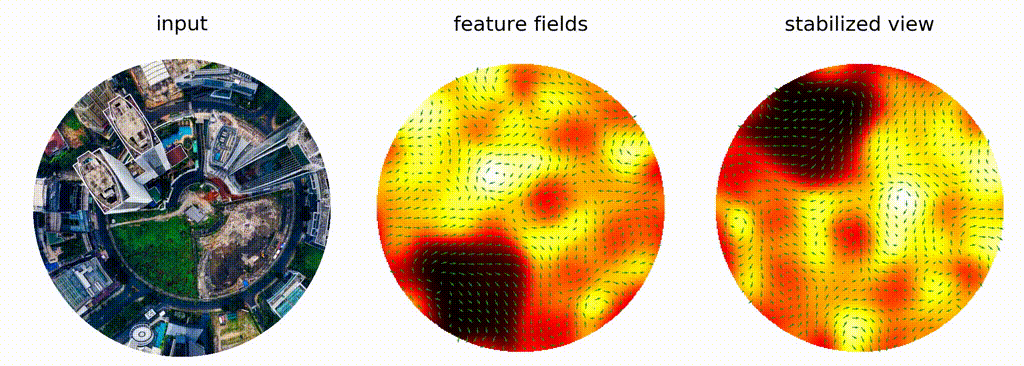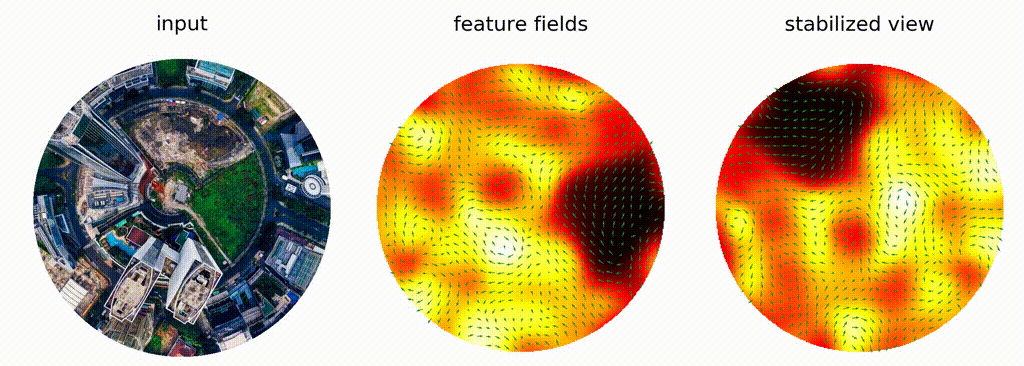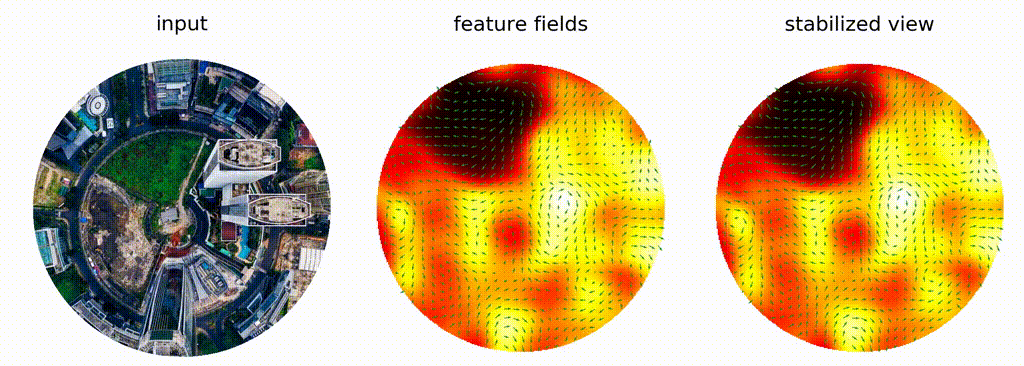
Equivariance (rotation) — Equivariance of a CNN w.r.t translation (left) and rotation (right). Transforming the image before and after a convolutional layer yields the same result.

The feature spaces of G-CNNs are described as collections of feature fields. Each field is essentially a feature map that assigns a tensor of values to each point in the input space. Common instances include scalar fields like grey-scale images and temperature distributions and vector fields such as wind velocity or electromagnetic fields. For example, one can think of feature vectors in standard CNNs as collections of \(N_{channels}\) scalar fields and generalize them to collections of fields with different types (e.g. \(N\) scalar channels, \(M\) vector channels).

Examples of fields of different types and their transformation under rotation.

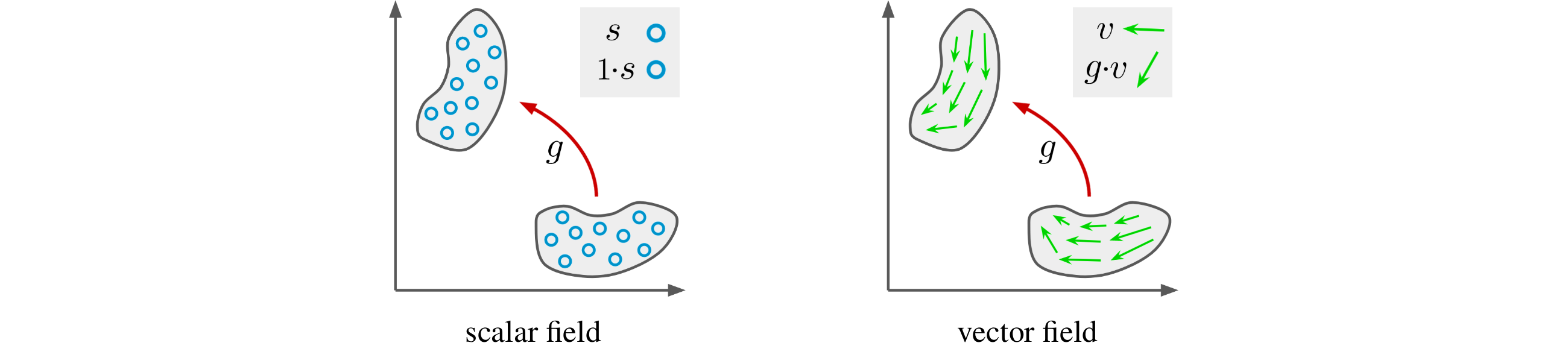
Depending on its type, a field has specific transformation behaviour when subjected to a group element, e.g. a rotation. This behaviour is described by a group representation, which is a mapping from group elements to linear operators on the field space. For example, a scalar field is invariant to rotation, and hence, the linear operator is the identity corresponding to the trivial representation. We furthermore must require that the model respects the transformation laws of input, intermediate and output feature fields, which is essentially the equivariance constraint covered next.

Steerable CNNs

Steerable CNNs employ a special kind of kernels designed to be equivariant under specific transformations, e.g. rotations or reflections, creating a more geometrically consistent and powerful modelling tool compared to standard CNNs. It is important to note that the equivariance to translations is already covered by the convolutional operation itself (same kernel is applied at each point). Furthermore, one only has to focus on the origin-preserving transformations \(g \in G\) when designing steerable kernels.

Generally speaking, the design procedure for Steerable CNNs is as follows. First, one must specify the target group \(G\) depending on the type of symmetry one wants to capture. Next, one has to choose representations that describe the transformation behaviour of the input and output feature fields. Finally, solving the \(G\)-equivariance constraint on the kernel space yields the necessary kernel basis. Unfortunately, the solution derived for one group does not generalize to another group \(G' \neq G \). Hence, we have to design a new kernel space for each group \(G\) we want to be equivariant to, which might not be trivial and generally quite cumbersome.

Implicit steerable kernels

To avoid developing a new kernel basis for each group \(G\) from scratch, we propose an alternative way of building steerable convolutions based on implicit neural kernels, i.e. convolutional kernels implemented as continuous functions parameterized by MLPs:

The recipe for a \(G\)-equivariant convolutional layer that maps between spaces of feature fields with representations \(\rho_{in}(g), \rho_{out}(g)\) is as follows:

Define the kernel input (arbitrary steerable features are supported); let us denote it as \(\rho_{k}\);
The output representation of the \(G\)-MLP is \(\rho_{in}(g) \otimes \rho_{out}(g)\);
Implement the \(G\)-MLP (for example, using the escnn library) with the input representation \(\rho_{k}\) and the output representation \(\rho_{in}(g) \otimes \rho_{out}(g)\);
Reshape the output of the implicit kernel and convolve it with a convolutional input.

We theoretically prove that if a kernel is parameterized by a \(G\)-equivariant MLP, then the resulting convolution is equivariant to the same group \(G\).

Advantages of implicit steerable kernels

The resulting framework has two core advantages:

Generalizability: It allows one to implement a Steerable CNN that is equivariant to any compact group \(G\) for which a \(G\)-equivariant MLP can be built.

Performance comparison of Steerable CNNs with implicit kernels (orange) and non-implicit steerable kernels ( Cesa et al. ) (blue) on the rotated ModelNet-40 dataset for different \(G\).

We found that using implicit kernels significantly improves the performance of Steerable CNNs compared to the baseline approach ( Cesa et al. ), which is based on the group restriction trick. Essentially, the group-restriction trick is a way to build steerable kernels for a subgroup \(G'\) of a group \(G\) when the kernels for \(G\) are already known. On the other hand, our method does not require any prior knowledge of the kernels for \(G\) and hence is more general. The only cases where we found implicit kernels to be slightly inferior or on par with the baseline approach is when the analytical (hence, optimal) solution is available, e.g. for \(SO(3)\) and \(O(3)\). However, there might be tasks for which analytically derived kernels are not expressive enough, which brings us to the next point.

Expressiveness: Contrary to standard steerable kernels, the framework allows us to inject geometric and physical quantities, increasing the expressiveness of Steerable CNNs.

Using implicit kernels instead of standard steerable and injecting them with bond and atom properties significantly improves the performance of Steerable CNNs on the QM9 dataset.

Standard steerable kernels are defined as a function of the relative position \( \vec{r} \). This might be somewhat limiting in terms of expressivity for specific tasks (imagine if you want to compute the free energy of a molecule, for which you might want to condition your kernels on the type of atoms, their charges, etc.). Furthermore, even if there are analytically derived kernels for a specific group \(G\), they might not be optimal for a specific task. Neural representation allows us to circumvent this limitation by conditioning the kernel on any task-specific features.

BibTeX


        @inproceedings{
          anonymous2023implicit,
          title={Implicit Convolutional Kernels for Steerable {CNN}s},
          author={Maksim Zhdanov and Nico Hoffmann and Gabriele Cesa},
          booktitle={Thirty-seventh Conference on Neural Information Processing Systems},
          year={2023},
          url={https://openreview.net/forum?id=2YtdxqvdjX}
          }