Erwin Transformer
We can organize irregular data (point clouds, meshes) using ball trees to enable sub-quadratic (sparse) attention. Fast and expressive!
Introduction
Since attention[1] was introduced in 2017, a natural scientific instinct was to try to address its most obvious drawback - quadratic complexity. Many approaches emerged, specifically in the context of text and images. The main reason why numerous solutions exist for text and images is the regular structure of data. That is, if I tell you to look at position/column $j$, you know exactly where to look. Same with relative positions - there is no ambiguity when it comes to computing distance between two tokens in a sequence or two pixels in an image. Therefore, one can exploit this structure and derive a fixed attention pattern that is guaranteed to respect the geometry of the domain.
Sparse attention exploits locality in regular data
Sparse Attention on Irregular Data
Now, when it comes to irregular structures such as point clouds or unstructured meshes, the task becomes harder since data do not have an inherent ordering. This means that $i$-th and $j$-th elements are never guaranteed to be at the same distance from one another across different data points. As we cannot rely on regularity anymore, there is seemingly nothing to exploit - and the only solution would be to buckle up, make GPUs go brr and compute full attention.
Sparse attention breaks locality in irregular data
Current Solutions in Physical Modelling
This solution is, however, unrealistic in physical modelling - the field I am interested in - for two reasons: A) all the GPUs are taken by LLM folks, B) the number of points might reach well beyond 1 million. Furthermore, there is clearly a need for sparse attention for large scale physical systems, despite the limited number of solutions available. The most popular approach so far involves pooling to latent tokens/supernodes (Transolver[2], UPT[3]), which makes the total cost sub-linear. Alternatively, one can project irregular data onto a regular domain, as one has full control over the latent node arrangement. This was done in Aurora[4] (and later in Appa[5]), which first uses Perceiver[6] for projection and then Swin Transformer[7] for handling attention over the latent regular grid, thus bringing the complexity down to log-linear. In between, there are solutions that have linear complexity and are based on turning a point cloud into a 1D sequence, e.g., via tree traversal (Octformer[8]) or space-filling curves (PointTransformer v3[9]).
Sub-quadratic attention for irregular data
The advantage of the last approach is that it operates on native geometry and does not introduce an information bottleneck with pooling. Working with full fidelity is much closer in spirit to what people typically do in language modelling - the ultimate scaling frontier - with recent advancements in pushing the resolution even further with byte-level tokenization[10]. In general, I believe that this is what should be done at scale for as long as possible - let the data guide the model to decide which information to use and which not.
Tree-based Attention
Therefore, the goal for the project was to find a solution that would allow operation on the original full-scale representation of a system, capture long-range interactions, but avoid quadratic scaling of full attention. This problem traces back to 1980s many-body physics, where physicists needed to simulate particle systems with long-range interactions (electrostatic/gravitational potentials) at the scale of tens of millions of nodes. To avoid computing all-to-all pairwise interactions ($\approx 10^{12}$ for 1M nodes), one can resort to approximations (e.g. Barnes-Hut algorithm). Specifically, if there are many particles far away from a single node, one can treat those particles as a cluster and compute cluster-node interaction instead of pairwise interactions. This can be done at multiple scales, thus extending the range of captured interactions and their resolution. The computation is typically structured using hierarchical trees. For mode detils, check out the fantastic blog by Andy Jones on the Fast Multipole Method, who also implemented it in PyTorch - well worth a read.
Many-body tree methods
This is the main idea behind Erwin - use hierarchical trees to impose regular structure on otherwise irregular data, then exploit this structure to organize attention and yield sub-quadratic complexity. Our first question was which tree to use. Traditionally, in many-body physics, octrees are used. These are built by recursively subdividing the cubic domain into sub-domains until each box contains at most a specified number of particles. This tree structure has even proved useful in the context of point cloud attention (see Octformer[8], which traverses the tree to turn the underlying point cloud into a sequence suitable for sparse attention). However, we did not pursue octrees as the partitions they form might be highly unbalanced when particles cluster. This is particularly apparent when working with molecular dynamics, as shown in the figure below.
Data-driven domain partitioning with trees
Ball Trees
On the contrary, ball trees, which we chose in the end, do not have this issue and are generally more robust to varying densities (although definitely not perfect, as we will see in the experiments later). Intuitively, the algorithm takes a bunch of points and covers them with a ball. Then, half of the points are covered with a smaller ball, and the remaining half with another ball such that no point belongs to both balls. The procedure is repeated until the smallest balls contain at most two points. You can now see why we chose to work with ball trees: they do not require covering the entire domain, only the points themselves, and at each tree level, the nodes are (often) associated with the same scale. This, in our opinion, makes ball trees an excellent candidate for handling irregular data, and we can now look at how they can be used to organize attention.
Iterative construction of Ball Tree
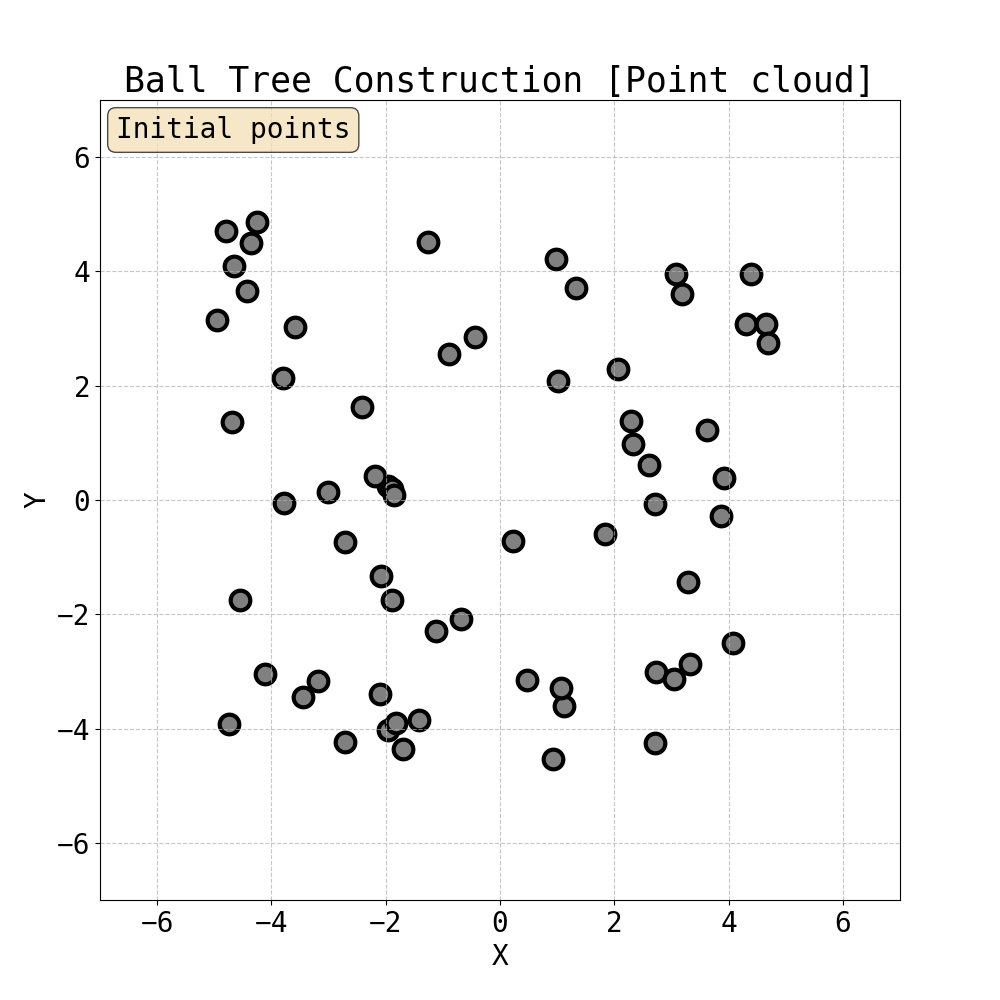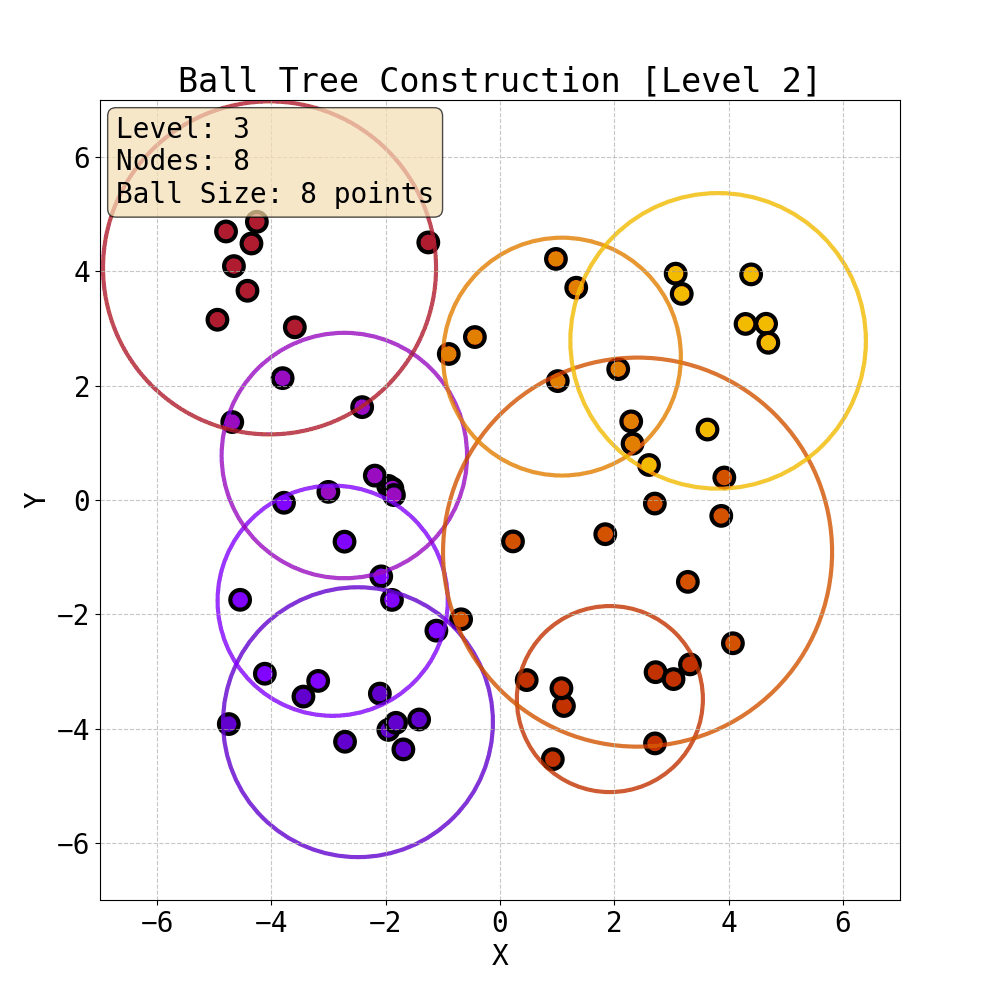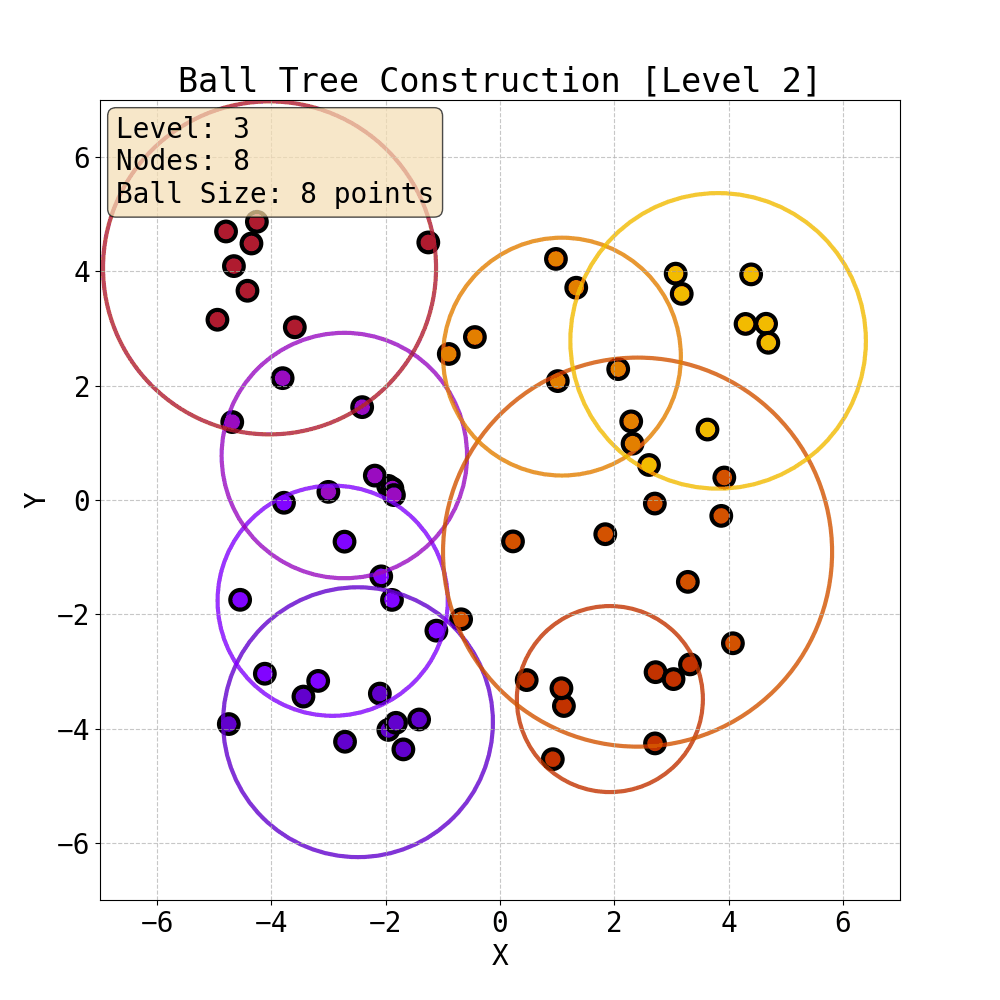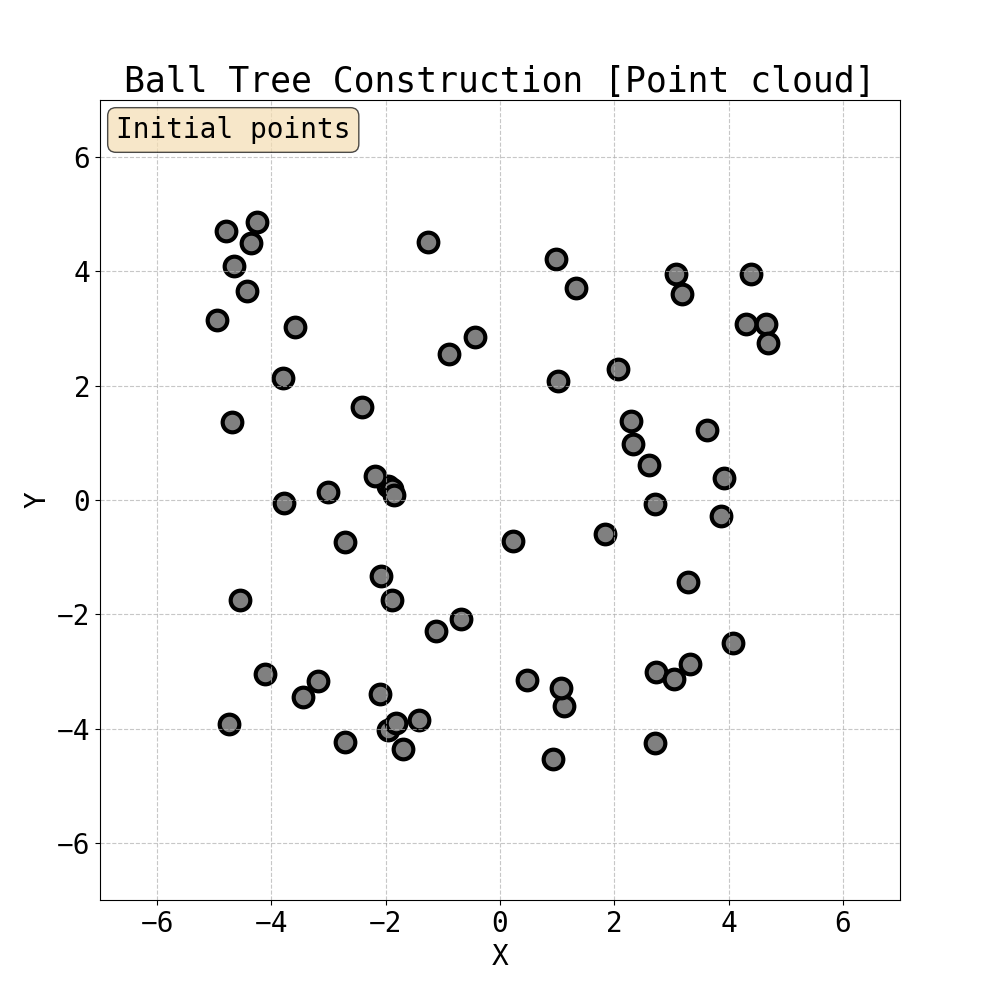
Having built a tree, we can now compute attention within the ball tree partitions. Specifically, one can choose the level of the tree and compute attention (Ball Tree Attention, BTA) within the balls in parallel. This is essentially block attention, but now each block is guaranteed to contain tokens that are close to each other in Euclidean space. This spatial locality is natural for physical systems where interactions typically decay with distance - nearby particles have stronger forces between them, and local features often exhibit spatial coherence. Therefore, by grouping neighbouring points together, BTA aligns with the intuition that the most important interactions are captured within each attention block. This is the attention mechanism we use to capture fine local details in data.
Attention is computed within ball partitions
Capturing Long-range Interactions
Now, obviously, block attention comes with a huge drawback - tokens cannot propagate information outside of their own blocks. This, of course, is unacceptable - we want to capture long-range interactions and hence have to introduce a mechanism for information to flow from one ball to another. We were inspired by Swin Transformer, which follows a very similar principle (the name Erwin is itself an homage to Swin Transformer, shifted windows $\rightarrow$ rotated windows). Specifically, while Swin uses sliding windows - essentially fixing the data and shifting the grid - we adapt the trick to irregular data. Specifically, we rotate the point cloud and build a second tree, exploiting the fact that ball tree construction is not rotation invariant, hence the new partitions will cover different groupings of points. By alternating between these two configurations in consecutive layers, we achieve information propagation beyond the original partitions.
Alternating between ball trees
For large particle systems, however, this strategy still has limited receptive field and might be prone to problems arising in message passing - oversmoothing and oversquashing. Therefore, to capture very long-range interactions, we coarsen the tree and implement the model UNet-style. This is done trivially by simply pooling points in leaf balls to their center of mass, which halves the number of nodes. A nice property of ball trees is that the pooled nodes will still be contained in the original partitions all the way up to the root, hence we do not have to rebuild it.
Information propagation via coarsening
Memory Layout of Erwin
Perhaps the nicest property of ball trees is how they are stored in memory. The memory layout is contiguous and nested, meaning that smaller partitions within the same ball are stored next to each other. This makes all the operations related to tree handling extremely efficient: to build balls, you simply reshape the data tensor, and to pool, you simply call the mean operation. With the computational overhead minimized, it really boils down to the attention operation and tree building, both of which have to be optimized.
Ball tree is stored in memory contiguously
Efficient Ball Tree implementation
Luckily for us, there are plenty of extremely smart people working on the latter, so we focused on optimizing ball tree construction. Let’s be honest, if we claimed that our sparse attention is faster than full attention, but it takes seconds to organize the data, no one would be impressed. So, to impress people, we had to rewrite the implementation of scikit-learn which, while very efficient due to being written in C, does not allow handling batches, i.e., you have to build a tree for each element sequentially. To overcome this limitation, we (with great help from Claude, frankly speaking) implemented the construction in C++ and OpenMP such that the construction is parallelized over CPU cores and we can handle batches all in parallel, even with different point cloud sizes within the batch. This greatly reduces the runtime by a factor of 6 to 20 depending on the size of point clouds:
Benchmarking Ball Tree construction
| Implementation | 1k nodes | 2k nodes | 4k nodes | 8k nodes | 16k nodes |
|---|---|---|---|---|---|
| sklearn + joblib | 15.6 ms | 16.3 ms | 21.2 ms | 24.1 ms | 44.0 ms |
| Ours | 0.32 ms | 0.73 ms | 1.54 ms | 3.26 ms | 6.98 ms |
| Speed-up | 48.8× | 22.3× | 13.8× | 7.4× | 6.3× |
Experiments
Now, for the fun part - experiments. Before we present tables with bold numbers, let’s highlight some technical details about Erwin’s key properties: efficiency and global receptive field. Tree building consistently accounts for only a minor fraction of total computation time and can be precomputed before training for static geometries. To address the most frequently asked question: yes, you need to rebuild the tree at each time step when points move, but this is manageable because (A) our optimized implementation is fast, and (B) all layers share the same tree, amortizing the construction cost.
Molecular Dynamics
When we first started the project, I had large molecular systems in mind as a primary application. So this is exactly where I started: with the dataset from Fu et al.[11], which contains dynamics of relatively large (coarse-grained, CG) polypeptides. The goal is to predict forces acting on each CG bead. As the main baseline we chose MPNN, which after some tuning turned out to be very tough to beat. In hindsight, this is not surprising as the dataset doesn’t have any charges, hence all the interactions are local. The experiment also confirmed to me just how good MPNNs are at picking up local interactions. In fact, we had to put a small MPNN before attention blocks to capture very fine local features - something that transformer alone wasn’t able to do (I wrote a recent thread about this on Twitter). Nonetheless, Erwin does push the Pareto frontier, mainly because of how fast it is at the scale of this dataset.
Standard PDE Benchmarks
Next, we benchmarked on a couple of PDE-related datasets - ShapeNet and datasets that people refer to as standard PDE benchmarks (specifically the ones that are not on regular grids, hence no Navier-Stokes or Darcy flow). Erwin shows incredibly strong performance on the majority of tasks but, interestingly, it fails on Airfoil - something that must be related to the structure of the mesh, where the density of points is decreasing moving away from the geometric center. We think this creates ball partitions with radically different densities, which complicates training. That being said, we never had issues with other non-uniform meshes. Another interesting finding was on the ShapeNet car dataset, where the strongest performance was achieved by models that did not involve any sort of pooling. That is, Erwin following a flat transformer structure (no coarse-graining of the tree) demonstrates state-of-the-art performance (for a sparse transformer, at least). This contrasts with other baselines that do involve pooling: GNO, UPT, Transolver. We attribute this to the sensitivity of the task to resolution - apparently one needs to work at full fidelity to capture all the necessary details.
Standard PDE benchmarks
| Model | Elasticity | Plasticity | Airfoil | Pipe |
|---|---|---|---|---|
| LNO | 0.69 | 0.29 | 0.53 | 0.31 |
| Galerkin | 2.40 | 1.20 | 1.18 | 0.98 |
| HT-Net | / | 3.33 | 0.65 | 0.59 |
| OFormer | 1.83 | 0.17 | 1.83 | 1.68 |
| GNOT | 0.86 | 3.36 | 0.76 | 0.47 |
| FactFormer | / | 3.12 | 0.71 | 0.60 |
| ONO | 1.18 | 0.48 | 0.61 | 0.52 |
| Transolver++ | 0.52 | 0.11 | 0.48 | 0.27 |
| Erwin (Ours) | 0.34 | 0.10 | 2.57 | 0.61 |
ShapeNet-Car
| Model | MSE |
|---|---|
| PointNet | 43.36 |
| GINO | 35.24 |
| UPT | 31.66 |
| Transolver | 19.88 |
| GP-UPT | 17.02 |
| PTV3-S | 19.09 |
| PTV3-M | 17.42 |
| Erwin-S (Ours) | 15.85 |
| Erwin-M (Ours) | 15.43 |
Turbulent Fluid Dynamics
The final experiment is the EAGLE dataset[12], which is a large-scale collection of turbulent fluid dynamics trajectories on irregular meshes of different shapes, approximately 3.5k nodes on average. There is nothing really interesting to say except for just how well a good model can learn and for how long it can unroll seemingly complex trajectories autoregressively. It was very impressive to see, and even better to see Erwin do it the best :).
RMSE on velocity V and pressure P fields across different prediction horizons
| Model | \(+\Delta t \) | \(+50\Delta t \) | Time (ms) |
Mem. (GB) |
||
|---|---|---|---|---|---|---|
| V | P | V | P | |||
| MGN | 0.081 | 0.43 | 0.592 | 2.25 | 40 | 0.7 |
| GAT | 0.170 | 64.6 | 0.855 | 163 | 44 | 0.5 |
| DRN | 0.251 | 1.45 | 0.537 | 2.46 | 42 | 0.2 |
| EAGLE | 0.053 | 0.46 | 0.349 | 1.44 | 30 | 1.5 |
| Erwin (Ours) |
0.044 ±0.001 |
0.31 ±0.01 |
0.281 ±0.001 |
1.15 ±0.06 |
11 | 0.2 |
Future Work
Regarding future work, there are definitely exciting directions to explore given how simple and even trivial the current attention pattern is, and how much more can be done by exploiting the ball tree structure to make the model more expressive. Below are two projects that I am working on with my students.
Erwin Meets Native Sparse Attention
To improve the processing of long-range informaition while keeping the cost sub-quadratic, we combine the ball tree with Native Sparse Attention (NSA) from DeepSeek, which align naturally with each other. Specifically, NSA allows Erwin to learn for each leaf node to which partitions to attend in the tree in a data-driven manner, thus extending interactions beyond fixed balls. We already have some promising results that I will be presenting at ICML 2025 Workshop on Long-Context Foundation Models, see the paper and the code.
Erwin for Industrial Scale Applications
Despite its linear complexity, applications involving simulations with tens of millions of particles currently remain beyond Erwin’s reach. To address this, we are exploring a hybrid approach: combining Transolver with Erwin by applying ball tree attention over latent tokens. The key insight is that by using Erwin to process these supernodes, we can afford larger bottleneck sizes (more supernodes) while maintaining efficiency. This allows us to significantly reduce the compression ratio compared to Transolver, preserving more information while keeping computational costs manageable. Initial results are promising - stay tuned!
BibTeX
If you find our work relevant to your research or found it otherwise useful, please consider citing us :)
@inproceedings{zhdanov2025erwin,
title={Erwin: A Tree-based Hierarchical Transformer for Large-scale Physical Systems},
author={Maksim Zhdanov and Max Welling and Jan-Willem van de Meent},
booktitle = {International {Conference} on {Machine} {Learning} ({ICML})},
year = {2025},
}